运筹学-第三、四章课堂作业
豆豆 2022-12-27 16:42:20 1801人已围观
1、第三章:EXCEL求解练习:ppt-DMD3—p8例1
例1:某工厂按合同规定必须于当年的每个季度末分别提供10、15、25、20台同一规格的柴油机。已知该厂的生产能力及生产每台柴油机的成本如表示。又如果生产出来的柴油机当季不交货,每台每积压一个季度需要存储维护费用0.15万元。要求在完成合同的情况下,做出使全年生产费用最小的决策。
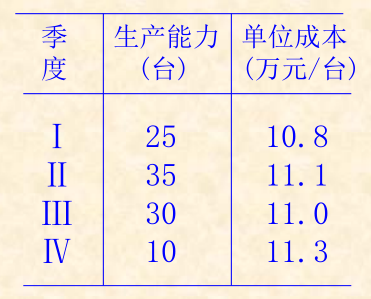
解答:
(1)、建模
设Xij(i=1,2,3,4; j=1,2,3,4)表示第i个季度生产,用于第j个季度销售的柴油机数量,表格表示如下:
| I | 1季度销售 | 2季度销售 | 3季度销售 | 4季度销售 |
| 1季度生产 | X11 | X12 | X13 | X14 |
| 2季度生产 | ----------- | X22 | X23 | X24 |
| 3季度生产 | ----------- | -------------- | X33 | X34 |
| 4季度生产 | ---------- | ---------- | ---------- | X44 |
目标函数:
min(z)=(X11+X12+X13+X14)*10.8+(X22+X23+X24)*11.1+(X33+X34)*11+X44*11.3+X12*0.15+X13*0.15+X14*0.15+X23*0.15+X24*0.15+X34*0.15
=10.8X11+10.95X12+10.95X13+10.95X14+11.1X22+11.25X23+11.25X24+11X33+11.15X34+11.3X44
约束条件:
生产:
X11+X12+X13+X14<=25 ; X22+X23+X24<=35 ;X33+X34<=30; X44<=10
Xij>=0(i=1,2,3,4; j=1,2,3,4)
销售:
X11=10 ;X12+X22=15 ;X13+X23+X33=25 ; X14+X24+X34+X44=20
(2)、excel求解
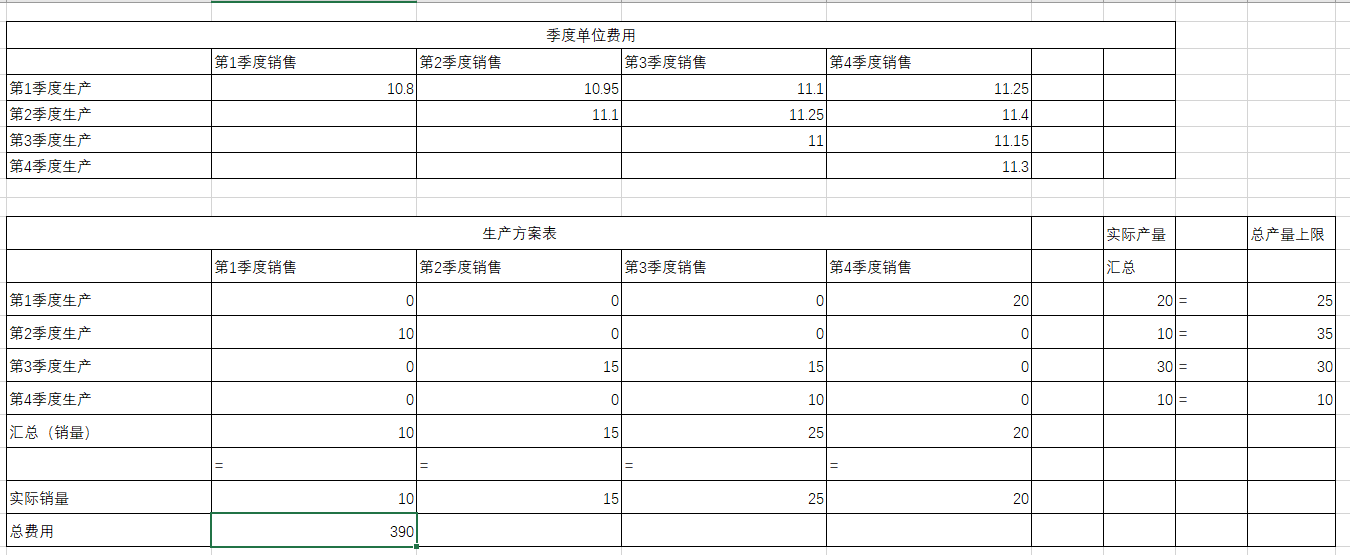
函数设置:
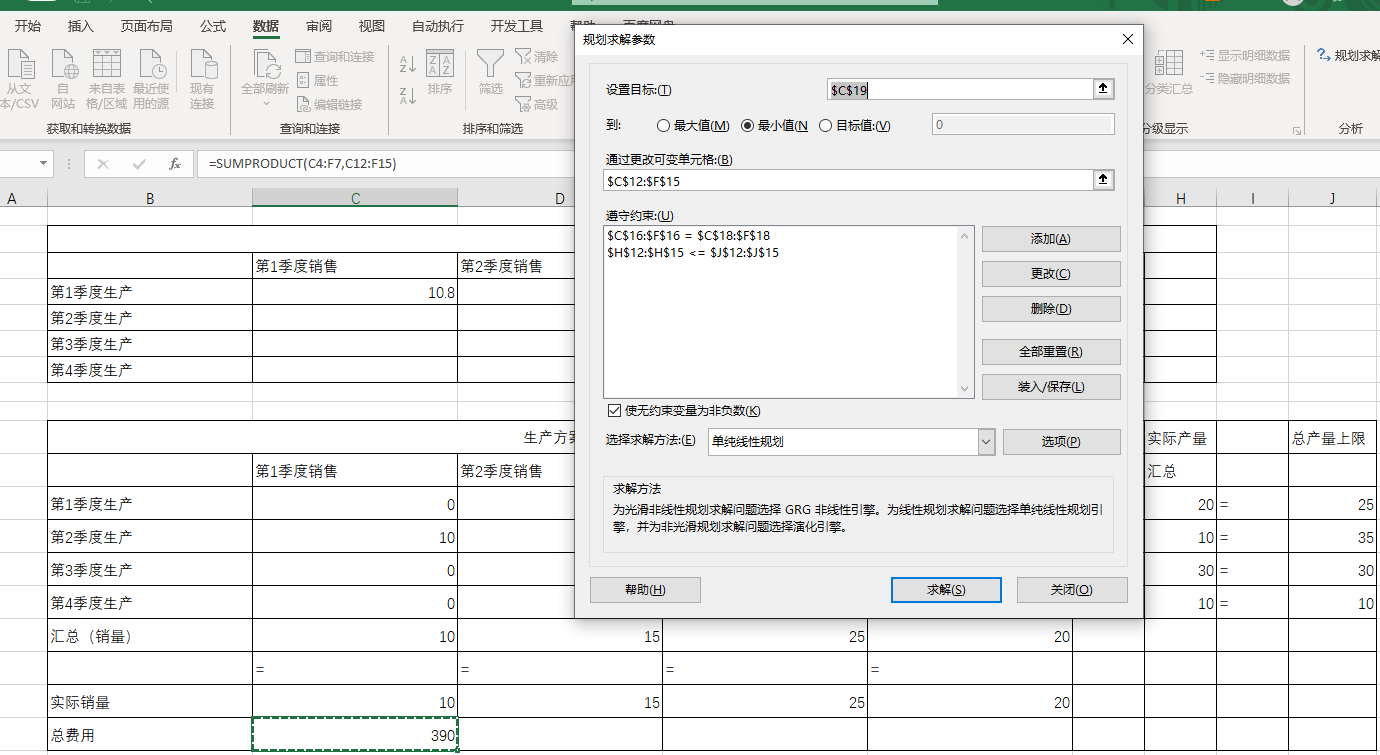
最优解:
X11=
X12=
X13=
X14=
X22=
X23=
X24=
X33=
X34=
X44=
Min(z)=390
2、第四章:EXCEL求解练习:ppt-DMD4—p21例1
例1:在未来四个月中,某制鞋厂必须按时完成下述合同要求,第一个月300双,第二个月500双,第三个月100双,第四个月100双。在一月初,工厂已有50双鞋(以前的存货)和3名工人,每名工人的月薪为1500元,每月可工作160小时(正常工作时间)。一名工人最多还可有20小时的加班工作时间(规定),在加班工作时,每小时需付25元的加班费用。制作一双鞋需耗费4个工时和5元的原料费。在每月的开始,可以租用和解雇工人。每雇用一名工人需支付1600元的费用,每解雇一名工人需支付2000元的解雇费用。在每月末,要为留在仓库里未交货的每双鞋支付30元的保管维护费用。一个月生产的产品可用于满足多个月的需求。试用ILP方法确定最佳的生产计划和用工政策。
分析:
1、需求量
| 月份 | 第1月 | 第2月 | 第3月 | 第4月 |
| 需求 | 300 | 500 | 100 | 100 |
| 雇佣 |
2、供应量
解答


解答
设Xij(i=1、2、3、4;j=1、2)
Yij,(i=1、2、3、4;j =1、2)
Zij(i=1、2、8、4;j =1、2)
其中:
Xi1为第i个月正常生产鞋的数量:
Xi2为第i个月加班生产鞋的数量;
Yi1:为第i个月正常生产的时间;
Yi2:为第i个月加班生产的时间;
Zi1:为第i个月新雇人数;
Zi2:为第i个月解雇人数(i=1、2、3、4)。
目标函数为:
min z= 30[(50+X11+X12-300)+(50+X11+X12-300+X21+X22-500)
+(50+X11+X12-300+X21+X22-500+X31+X32-100)]+1600[(3
+Z11-Z12)+(3+Z11-Z12+Z21-Z22)+(3+Z11-Z12 +Z21-Z22+Z31-Z32)+(3+Z11-Z12+Z21-Z22+Z31+Z41Z42)]+5(X12+X22+X32+X42)
+1600(Z11+Z21+Z31+Z41)+2000(Z21+Z22+Z23+Z24) +25(Y12+Y22+Y32+Y42)
约束条件:
50+X11+X12>=300
50+X11+X12-300+X21+X22>=500
50+X11+X12-300+X21+X22-500+X31+X32>=100
50+X11+X12-300+X21+X22-500+X31+X32-100>=100
4X12<=Y12
4X22<=Y22
4X32<=Y32
4X42<=Y42
4X11<=Y11
4X21<=Y21
4X31<=Y31
4X41<=Y41
3+Z11-Z12>=0
3+Z11-Z12+Z21-Z22>=0
3+Z11-Z12+Z21-Z22+Z31-Z32>=0
3+Z11-Z12+Z21-Z22+Z31-Z32+Z41-Z42>=0
Xij,Yij,Zij≥0且为整数
i=1、2、3、4
j=1、2
3、第四章:EXCEL求解练习:ppt-DMD4 p25例2
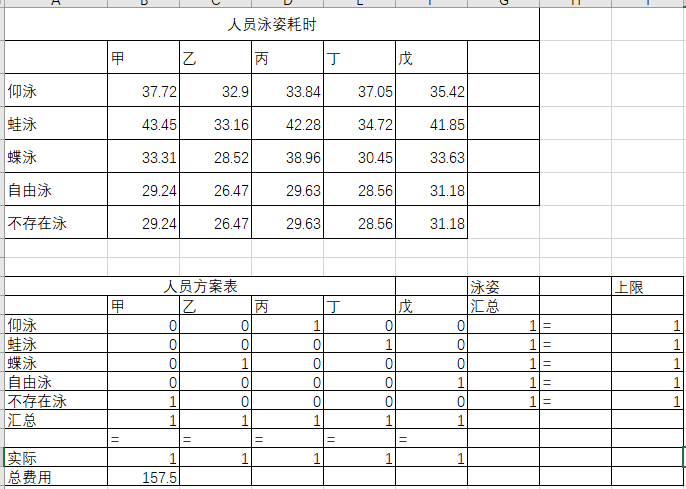
游泳队的教练要从甲、乙、丙、丁、戊5名运动员中选出4名运动员组成一个4x100混合泳接力队,已知个人的各种泳姿成绩如表示,问:应选择那些运动员,怎样安排?
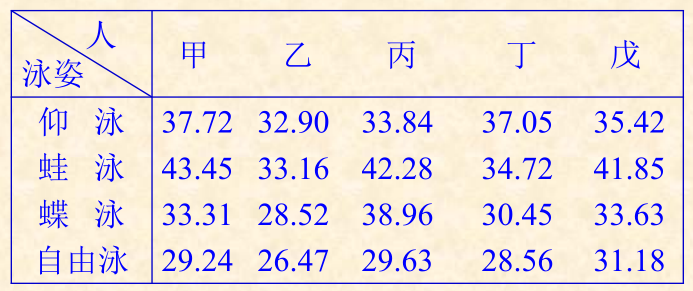
解答:
(1)、建模
设Xij(i=1-甲,2-乙,3-丙,4-丁,5-戊;j=1-仰泳,2-蛙泳,3-蝶泳,4-自由泳)为0表示对于不选择,为1表示对应需要选择
目标函数
min(z)=37.72X11+43.45X12+33.31X13+29.24X14+32.9X21+33.16X22+28.52X23+26.47X24+33.84X31+42.28X32+38.96X33+29.63X34+37.05X41+34.72X42+30.45X43+28.56X44+
35.42X51+41.85X52+33.63X53+31.18X54
约束条件:
人的维度:
甲:X11+X12+X13+X14=1 ;乙:X21+X22+X23+X24=1 ;丙:X31+X32+X33+X34=1;丁:X41+X42+X43+X44=1 ;X51+X52+X53+X54=1
泳姿:
仰泳:X11+X21+X31+X41+X51=1,蛙泳:X12+X22+X32+X42+X52=1,蝶泳:X13+X23+X33+X43+X53=1,自由泳:X14+X24+X34+X44+X54=1
Xij=0或1(i=1,2,3,4,5;j=1,2,3,4)
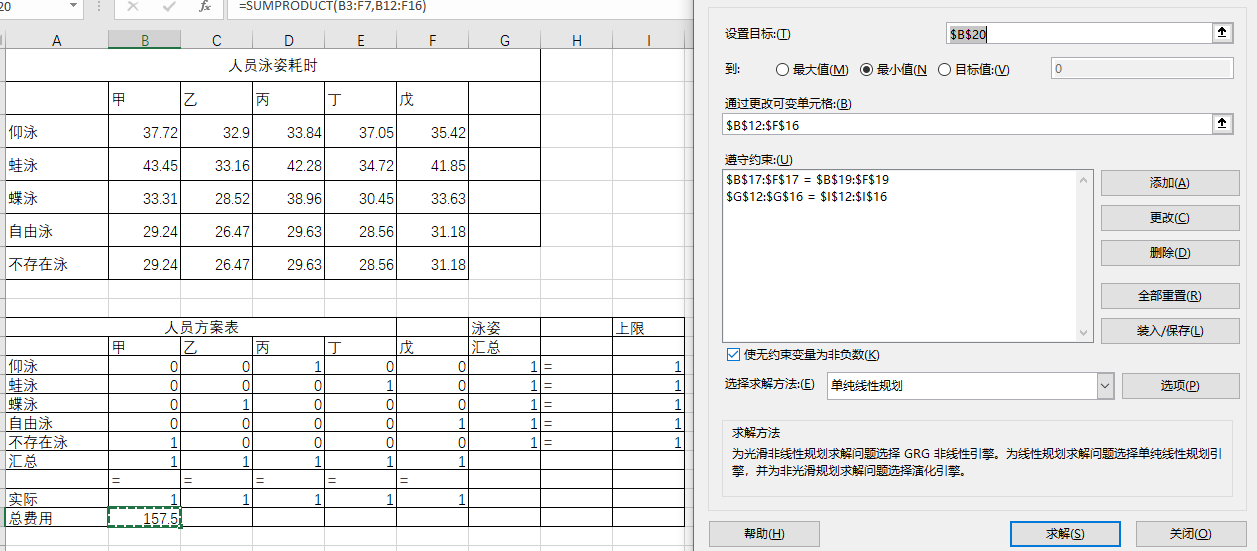
(2)、EXCEL求解
4、第四章:教材《运筹学基础及应用》(第七版)-p115-4.1

解答:
(a)、X1+X2<=2+My ;2X1+3X2>=5-M(1-y) ; y=0或者1
(b)、X=3y1+5y2+7y3 ;y1+y2+y3<=1;yi=0或1(i=1,2,3)
(c)、X=0+My X>=50-(1-y)M ;y=0或者1
(d)、X1<=2+My ;X2>=1-My ; y=0或者1 且 X1>=2-M(1-y) ;X2<=4+M(1-y)
(e)、X1+X2<=5+My1 ;X1<=2+My2; X3>=2+My3 ;X3+X4>=6+My4 ;y1+y2+y3+y4<=2 ;yi=0或1(i=1,2,3,4)
(f)、0<=x<=2000y ;1000-x<=2000(1-y) ;y=0或1
5、第四章:教材《运筹学基础及应用》(第七版)-p115-4.2(如上图)

解答:
(1)设yi(i=1...10)为0表示不选中,为1表示选中;
(2)、目标函数:min(z)=c1*y1+c2*y2+c3*y3+c4*y4+c5*y5+c6*y6+c7*y7+c8*y8+c9*y9+c10*y10
(3)、约束条件
y1+y8=1 ;y7+y8=1
y3+y5<=1;y5+y4<=1
y2+y6+y9+y10<=2
y1+y2+y3+y4+y5+y6+y7+y8+y9+y10=5;
yi(i=1...10)=0或1

 备付金存管银行是指可以为支付机构办理客户备付金的跨行收付业务,并负责对支付机构存放在所有备付金银行的客户备付金信息进行归集、核对与监督的备付金银行。(支付机构客
备付金存管银行是指可以为支付机构办理客户备付金的跨行收付业务,并负责对支付机构存放在所有备付金银行的客户备付金信息进行归集、核对与监督的备付金银行。(支付机构客 首先需要知道什么叫一元购? 就是你支付一元后获得一个购物资格,有的叫抽
首先需要知道什么叫一元购? 就是你支付一元后获得一个购物资格,有的叫抽 最近有一套生产系统的数据库CPU老是偏高,发现闲时也在40%-60%左右,感觉很不正常,决定优化一下,在这
最近有一套生产系统的数据库CPU老是偏高,发现闲时也在40%-60%左右,感觉很不正常,决定优化一下,在这