运筹学-LP线性规划建模第一章课堂作业
豆豆 2022-12-04 23:52:02 739人已围观
第一、个人作业要求
作业:教材《运筹学基础及应用》(第七版):p43-1.1-(a)、(b),
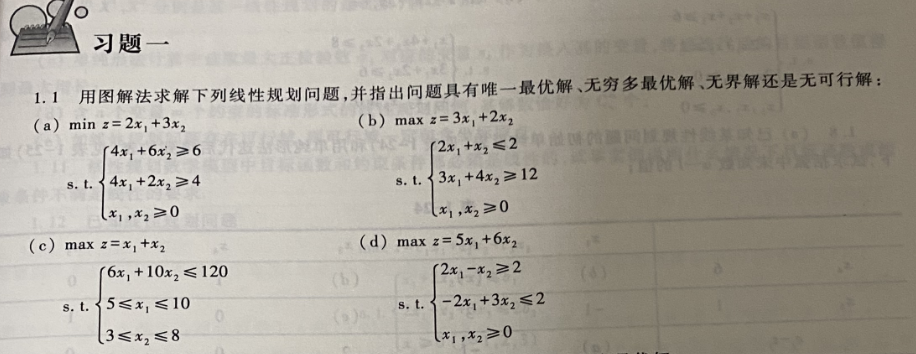
(a)、解答
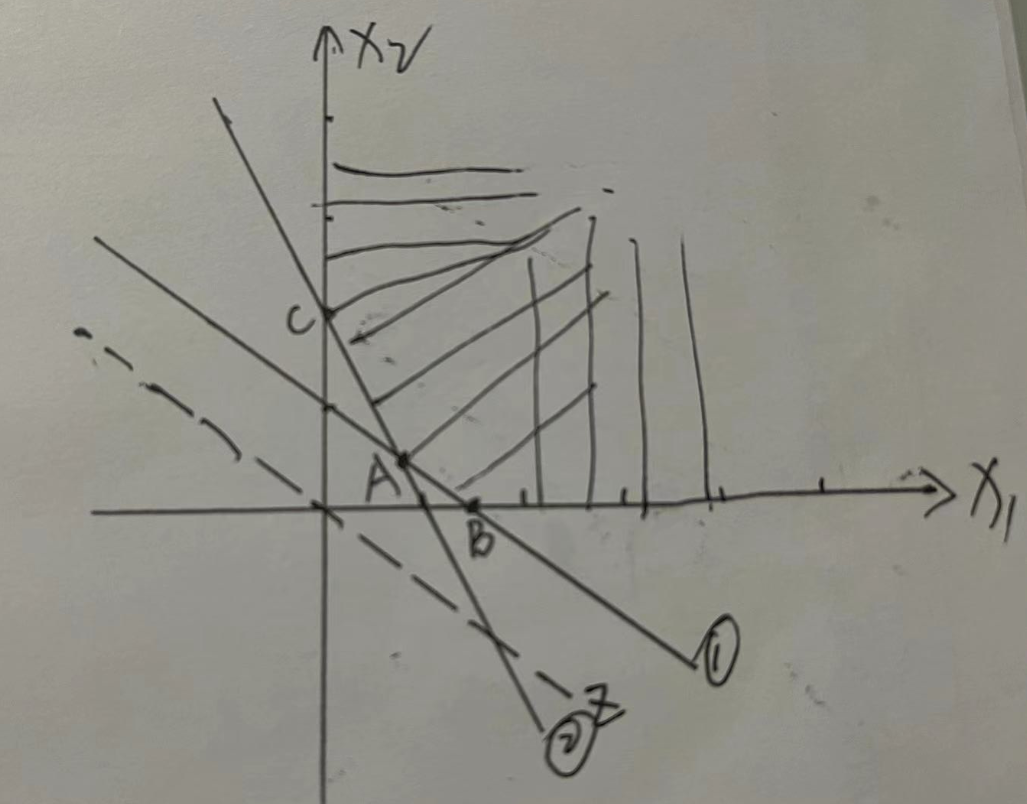
Z目标函数与直线1重叠,所以有无穷多最优解,在AB线上;
lindo验证结果:
(b)、解答
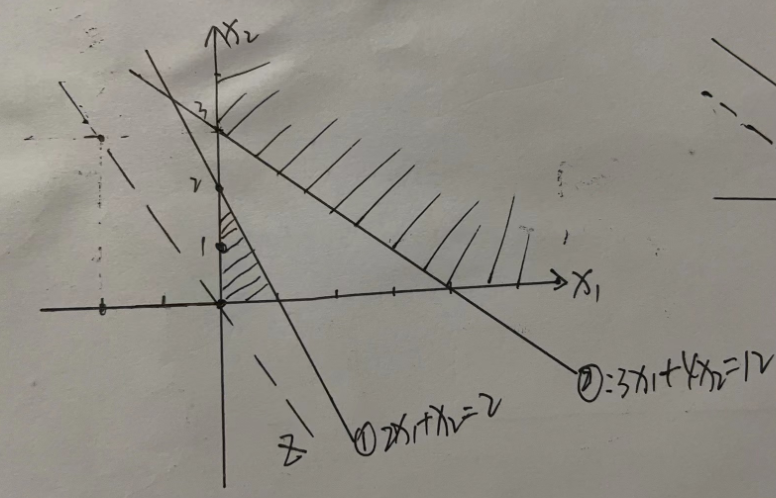
无可行解
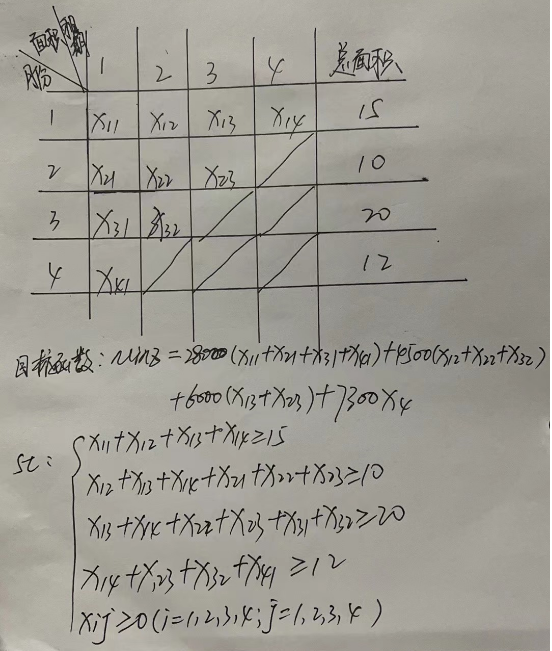
p45-1.14(只建模),


解:设该厂第i个月办理租借合同,租借j个月的面积为Xij,则该问题的线性规划模型为:
p46-1.16,(只建模)
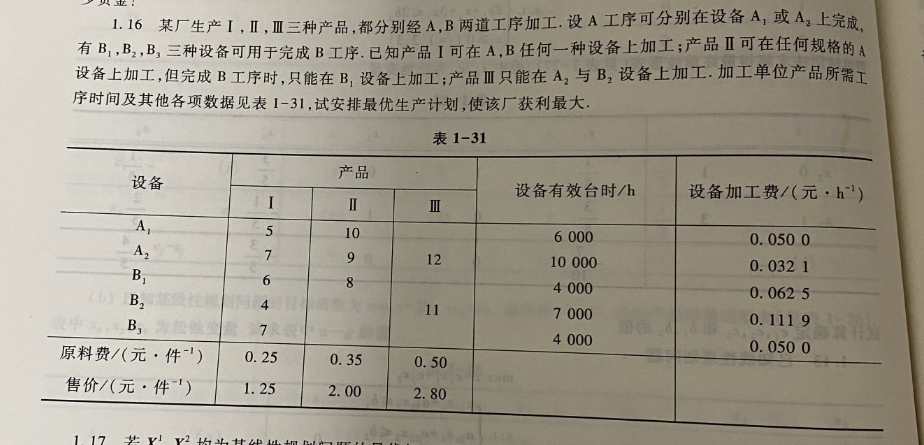
建模:
设设备编号:A1=1,A2=2,B1=3,B2=4,B3=5;设Xij表示第i个设备上生产的j种产品,变量分布如下图:
| I | 11 | 111 | |
| A1(1) | X11 | X12 | |
| A2(2) | X21 | X22 | X23 |
| B1(3) | X31 | X32 | |
| B1(4) | X41 | X43 | |
| B1(5) | X51 |
目标函数:
max(z)=(1.25-0.25)(X11+X21)+(2-0.35)(X12+X22)+(2.8-0.5)*X23-(5X11+10X21)*0.05-(7X21+9X22+12X23)*0.0321-(6X31+8X32)*0.0625-(4X41+11X43)*0.1119-7X51*0.05
约束条件:
X11+X21=X31+X41+X51
X12+X22=X32
X23=X43
5X11+10X12<=6000
7X21+9X22+12X23<=10000
6X31+8X32<=4000
4X41+11X43<=7000
7X51<=4000
Xij>=0(i=1,2,3,4,5;j=1,2,3)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
p-1.21(只建模);
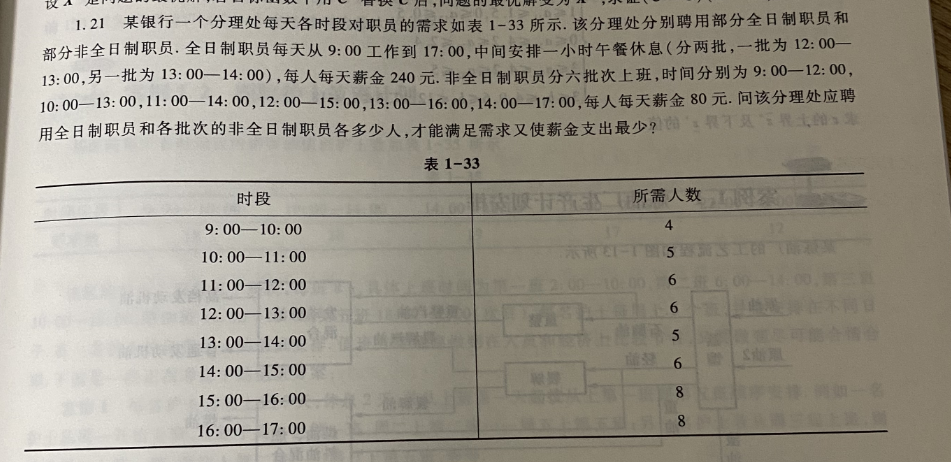
建模:
设全职X1人,非全职:9-12点上班:X2人,10-13点上班:X3人,11-14点上班:X4人,12-15点上班:X5人,13-16点上班:X6人,14-17点上班:X7人
则变量分布如下:
| 上班时段 | 全职上班人数 | 非全职人数 | 总需求量 |
| 9-10 | X1 | X2 | 4 |
| 10-11 | X1 | X2+X3 | 5 |
| 11-12 | X1 | X2+X3+X4 | 6 |
| 12-13 | 0.5X1 | X3+X4+X5 | 6 |
| 13-14 | 0.5X1 | X4+X5+X6 | 5 |
| 14-15 | X1 | X5+X6+X7 | 6 |
| 15-16 | X1 | X6+X7 | 8 |
| 16-17 | X1 | X7 | 8 |
目标函数:
min(z)=240X1+80(X2+X3+X4+X5+X6+X7)
约束条件:
X1+X2>=4
X1+X2+X3>=5
X1+X2+X3+X4>=6
0.5X1+X3+X4+X5>=6
0.5X1+X4+X5+X6>=5
X1+X5+X6+X7>=6
X1+X6+X7>=8
X1+X7>=8
Xi>=0(i=1,2...7)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
教材p72-2.1(a)、(b)

(a)、解答:
设置变量 :y1,y2,y3,
对偶目标函数:max(w)=2Y1+3Y2+5Y3;
约束条件:
Y1+2Y2+Y3<=2;
3Y1+Y2+4Y3<=2
4Y1+3Y2+3Y3=4;
Y1>=0,Y2<=0;Y3无约束
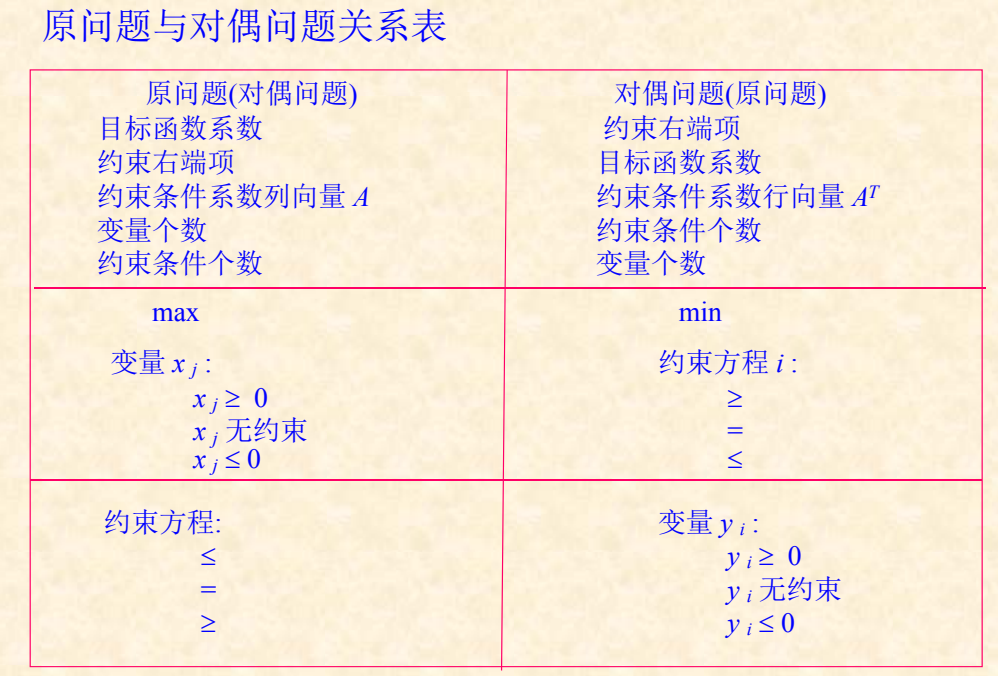
注意事项:这里是min,所以他的关系是反过来的,正常情况下是max转min对偶,所以这里需要参照对照表逆向处理:
(b)、解答:
设置变量:y1,y2,y3,
对偶目标函数:min(w)=5Y1+3Y2+8Y3;
约束条件:
Y1-Y2+4Y3=5;
2Y1+5Y2+7Y3>=6
2Y1-Y2+3Y3<=3;
Y1无约束,Y2<=0;Y3>=0
参考答案:https://www.onekbit.com/dwz/231
参考资料:
1、https://www.docin.com/p-1131637845.html
2、https://zhuanlan.zhihu.com/p/392190204

 备付金存管银行是指可以为支付机构办理客户备付金的跨行收付业务,并负责对支付机构存放在所有备付金银行的客户备付金信息进行归集、核对与监督的备付金银行。(支付机构客
备付金存管银行是指可以为支付机构办理客户备付金的跨行收付业务,并负责对支付机构存放在所有备付金银行的客户备付金信息进行归集、核对与监督的备付金银行。(支付机构客 首先需要知道什么叫一元购? 就是你支付一元后获得一个购物资格,有的叫抽
首先需要知道什么叫一元购? 就是你支付一元后获得一个购物资格,有的叫抽 最近有一套生产系统的数据库CPU老是偏高,发现闲时也在40%-60%左右,感觉很不正常,决定优化一下,在这
最近有一套生产系统的数据库CPU老是偏高,发现闲时也在40%-60%左右,感觉很不正常,决定优化一下,在这